![]() An
experimental evidence on the validity of third Smarandache conjecture.
An
experimental evidence on the validity of third Smarandache conjecture.
Felice Russo
Micron Technology Italy
Avezzano (Aq) – Italy
Abstract
In this note we report the results regarding the
check of the third Smarandache conjecture on primes [1],[2] for ![]() and
and ![]() . In the range analysed the
conjecture is true. Moreover, according to experimental data obtained,
it seems likely that the conjecture is true for all primes and for all
positive values of k..
. In the range analysed the
conjecture is true. Moreover, according to experimental data obtained,
it seems likely that the conjecture is true for all primes and for all
positive values of k..
Introduction
In [1] and [2] the following function has been defined:
![]()
where ![]() is the nth prime and k is a positive integer. Moreover in the above mentioned
papers the following conjecture has been formulated by F. Smarandache:
is the nth prime and k is a positive integer. Moreover in the above mentioned
papers the following conjecture has been formulated by F. Smarandache:
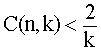 for
for ![]()
This conjecture is the generalization of the Andrica
conjecture (k=2) [3] that has not yet been proven. The Smarandache conjecture
has been tested for ![]() ,
, ![]() and in this note the result of this search is reported. The computer code
has been written utilizing the Ubasic software package.
and in this note the result of this search is reported. The computer code
has been written utilizing the Ubasic software package.
Experimental Results
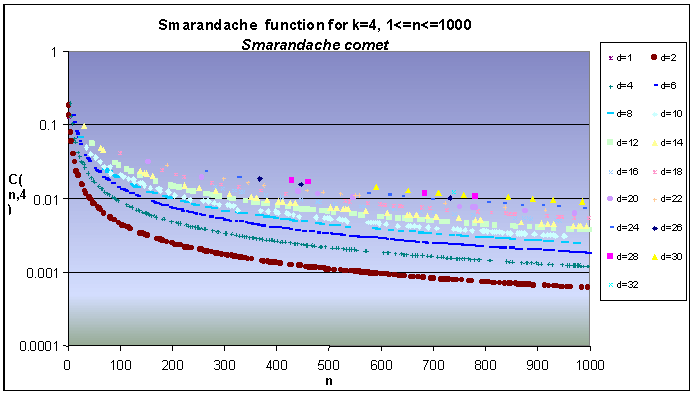
![]() In In the following graph
the Smarandache function for k=4 and n<1000 is reported. As we can see
the value of C(k,n) is modulated by the prime’s gap indicated by
In In the following graph
the Smarandache function for k=4 and n<1000 is reported. As we can see
the value of C(k,n) is modulated by the prime’s gap indicated by ![]() .
.
We call this graph the Smarandache "comet".
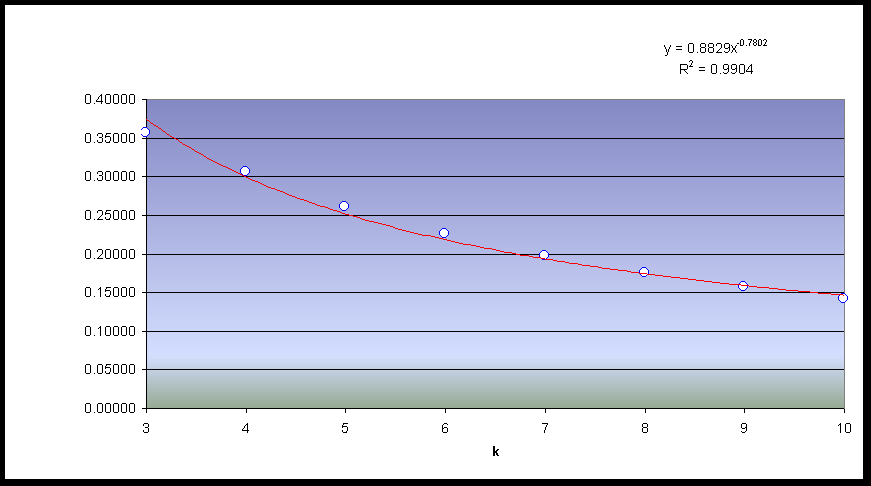
In the following table, instead, we report:
| the largest value Max_C(n,k) of Smarandache function for | |
| the difference | |
| the value of | |
| the value of 2/k |
|
k |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Max_C(n,k) |
0.67087 |
0.31105 |
0.19458 |
0.13962 |
0.10821 |
0.08857 |
0.07564 |
0.06598 |
0.05850 |
|
|
0.32913 |
0.35562 |
0.30542 |
0.26038 |
0.22512 |
0.19715 |
0.17436 |
0.15624 |
0.14150 |
|
|
7 |
7 |
7 |
7 |
7 |
3 |
3 |
3 |
3 |
|
2/k |
1 |
0.666.. |
0.5 |
0.4 |
0.333.. |
0.2857.. |
0.25 |
0.222.. |
0.20 |
According to previous data the Smarandache conjecture
is verified in the range of k and ![]() analysed due to the fact that
analysed due to the fact that ![]() is always positive.
is always positive.
Moreover since the Smarandache function falls
asymptotically as n increases it is likely that the estimated maximum
is valid also for ![]() .
.
We can also analyse the behaviour of difference
![]() versus the k parameter that
in the following graph is showed with white dots. We have estimated an
interpolating function:
versus the k parameter that
in the following graph is showed with white dots. We have estimated an
interpolating function:
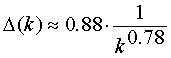 for k>2
for k>2
with a very good ![]() value
(see the continuous curve). This result reinforces the validity of Smarandache
conjecture since:
value
(see the continuous curve). This result reinforces the validity of Smarandache
conjecture since:
![]()
![]()
![]()
New Question
According to previous experimental data can we reformulate the Smarandache conjecture with a more tight limit as showed below?
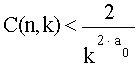
where ![]() and
and ![]() is the Smarandache constant
[4],[1].
is the Smarandache constant
[4],[1].
References
[1] See http://www.gallup.unm.edu/~smarandache/ConjPrim.txt
[2] Smarandache, Florentin, "Conjectures which Generalize Andrica's Conjecture", Arizona State
University, Hayden Library, Special Collections, Tempe, AZ, USA.
[3] see: "Andrica’s conjecture" in http://www.treasure-troves.com/math/
[4] N. Sloane, Seq. A038458 ("Smarandache Constant" = .5671481302020177146468468755...)
in <An On-Line Version of the Encyclopedia of Integer Sequences>,
http://www.research.att.com/cgi-bin/access.cgi/as/njas/sequences/ eishis.cgi.