On the Pseudo-Smarandache Function
By
J. Sįndor
Babes-Bolyai Univ., 3400 Cluj, Romania
![]()
Kashihara[2] defined the "Pseudo-Smarandache" function Z by
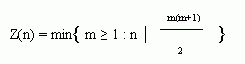
Properties of this function have been studied in [1], [2] etc.
1. By answering a question by C. Ashbacher, Maohua Le proved that S(Z(n)) - Z(S(n)) changes signs infinitely often. Put
We will prove first that
and
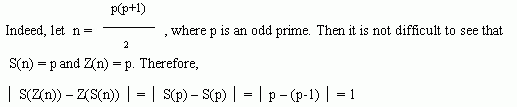
implying (1) . We note that if the equation S(Z(n)) = Z(S(n)) has infinitely many solutions, then clearly the lim inf in (1) is 0, otherwise is 1, since
| S(Z(n)) - Z(S(n)) | >= 1, S(Z(n)) - Z(S(n)) being an integer.
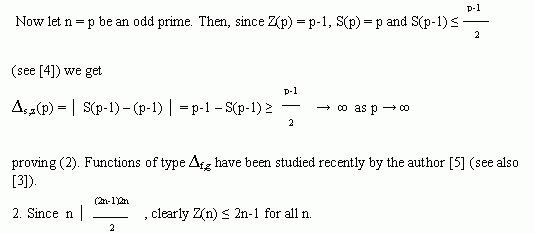
This inequality is best possible for even n, since Z(2k) = 2k+1 - 1. We note that for odd n, we have Z(n) <= n - 1, and this is best possible for odd n, since
By
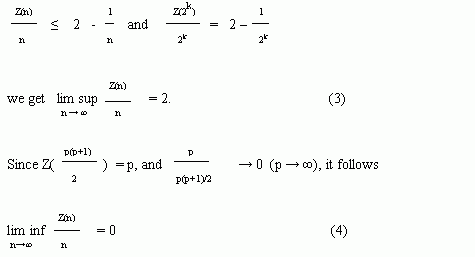

On the other hand, by Z(Z(n)) <= 2Z(n) - 1 and (3), we have
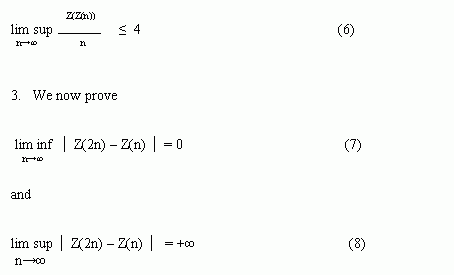
Indeed, in [1] it was proved that Z(2p) = p-1 for a prime p congruent to 1 modulo 4. Since
On the other hand, let n = 2k. Since Z(2k) = 2k+1 - 1 and
References
1. C. Ashbacher, The Pseudo-Smarandache Function and the Classical Functions of Number Theory, Smarandache Notions J., 9(1998), No. 1-2, 78-81.2. K. Kashihara, Comments and Topics on Smarandache Notions and Problems, Erhus Univ. Press, AZ., 1996.
3. M. Bencze, OQ. 351, Octogon M.M. 8(2000), No. 1, p. 275.
4. J. Sįndor, On Certain New Inequalities and Limits for the Smarandache Function, Smarandache Notions J., 9(1998), No. 1-2, 63-69.
5. J. Sįndor, On the Difference of Alternate Compositions of Arithmetical Functions, to appear.
|
|