![]() Some
results about four Smarandache U-product sequences
Some
results about four Smarandache U-product sequences
Felice
Russo
Micron Technology Italy
Avezzano (Aq) Italy
Abstract
In this paper four Smarandache product sequences have
been studied: Smarandache Square product sequence, Smarandache Cubic product
sequence, Smarandache Factorial product sequence and Smarandache Palprime
product sequence. In particular the number of primes, the convergence value for
Smarandache Series, Smarandache Continued Fractions, Smarandache Infinite
product of the mentioned sequences has been calculated utilizing the Ubasic
software package. Moreover for the first time the notion of Smarandache
Continued Radicals has been introduced. One conjecture about the number of
primes contained in these sequences and new questions are posed too.
Introduction
In [1] Iacobescu describes the so called
Smarandache U-product sequence.
Let ![]()
![]() , be a
positive integer sequence. Then a U-sequence is defined as follows:
, be a
positive integer sequence. Then a U-sequence is defined as follows:
![]()
In this paper differently from [1], we will call
this sequence a U-sequence of the first kind because we will introduce for the
first time a U-sequence of the second kind defined as follows:
![]()
In this paper we will discuss about the
"Square product", "Cubic product", "Factorial
product" and "Primorial product" sequences. In particular we
will analyze the question posed by Iacobescu in [1] on the number of primes
contained in those sequences. We will also analyze the convergence values of
the Smarandache Series [2], Infinite product [3], Simple Continued Fractions
[4] of the four sequences. Moreover for the first time we will introduce the
notion of Smarandache Continued Radicals and we will analyse the convergence of
sequences reported above.
Sequences details
o Smarandache square product sequence of the
first and second kind.
In this case the sequence ![]() is given by:
is given by:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144
that is the square of n. The first 20 terms of the
sequence ![]() (
(![]() ) both the first and second
kind are reported in the table below:
) both the first and second
kind are reported in the table below:
|
Smarandache Square product sequence (first kind) |
Smarandache Square product sequence (second kind) |
|
2 |
0 |
|
5 |
3 |
|
37 |
35 |
|
577 |
575 |
|
14401 |
14399 |
|
518401 |
518399 |
|
25401601 |
25401599 |
|
1625702401 |
1625702399 |
|
131681894401 |
131681894399 |
|
13168189440001 |
13168189439999 |
|
1593350922240001 |
1593350922239999 |
|
229442532802560001 |
229442532802559999 |
|
38775788043632640001 |
38775788043632639999 |
|
7600054456551997440001 |
7600054456551997439999 |
|
1710012252724199424000001 |
1710012252724199423999999 |
|
437763136697395052544000001 |
437763136697395052543999999 |
|
126513546505547170185216000001 |
126513546505547170185215999999 |
|
40990389067797283140009984000001 |
40990389067797283140009983999999 |
|
14797530453474819213543604224000001 |
14797530453474819213543604223999999 |
|
5919012181389927685417441689600000001 |
5919012181389927685417441689599999999 |
o Smarandache cubic product sequence of the
first and second kind.
In this case the sequence ![]() is given by:
is given by:
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331,
1728
that is the cube of n. Here the first 17 terms for
the sequence![]() of the
first and second kind.
of the
first and second kind.
|
Smarandache Cubic product sequence (first kind) |
Smarandache Cubic product sequence (second kind) |
|
2 |
0 |
|
9 |
7 |
|
217 |
215 |
|
13825 |
13823 |
|
1728001 |
1727999 |
|
373248001 |
373247999 |
|
128024064001 |
128024063999 |
|
65548320768001 |
65548320767999 |
|
47784725839872001 |
47784725839871999 |
|
47784725839872000001 |
47784725839871999999 |
|
63601470092869632000001 |
63601470092869631999999 |
|
109903340320478724096000001 |
109903340320478724095999999 |
|
241457638684091756838912000001 |
241457638684091756838911999999 |
|
662559760549147780765974528000001 |
662559760549147780765974527999999 |
|
2236139191853373760085164032000000001 |
2236139191853373760085164031999999999 |
|
9159226129831418921308831875072000000001 |
9159226129831418921308831875071999999999 |
|
44999277975861761160390291002228736000000001 |
44999277975861761160390291002228735999999999 |
o Smarandache factorial product sequence of
the first and second kind.
In this case the sequence ![]() is given by:
is given by:
1, 2, 6, 24, 120, 720, 5040, 40320, 362880
.
that is the factorial of n. The first 13 terms of
the![]() sequence of the
first and second kind follow.
sequence of the
first and second kind follow.
|
Smarandache Factorial product sequence (first kind) |
Smarandache Factorial product sequence (second kind) |
|
2 |
0 |
|
3 |
1 |
|
13 |
11 |
|
289 |
287 |
|
34561 |
34559 |
|
24883201 |
24883199 |
|
125411328001 |
125411327999 |
|
5056584744960001 |
5056584744959999 |
|
1834933472251084800001 |
1834933472251084799999 |
|
6658606584104736522240000001 |
6658606584104736522239999999 |
|
265790267296391946810949632000000001 |
265790267296391946810949631999999999 |
|
127313963299399416749559771247411200000000001 |
127313963299399416749559771247411199999999999 |
|
792786697595796795607377086400871488552960000000000001 |
792786697595796795607377086400871488552959999999999999 |
o Smarandache primorial product sequence of
the first and second kind.
In this case the sequence ![]() is given by:
is given by:
2, 3, 5, 7, 11, 101, 121,131, 151, 181, 191, 313,
353, 353, 373
that is the sequence of palindromic primes. Below
the first 17 terms of the ![]() sequence of the first and second kind.
sequence of the first and second kind.
|
Smarandache Palprime product sequence (first kind) |
Smarandache Palprime product sequence (second kind) |
|
3 |
1 |
|
7 |
5 |
|
31 |
29 |
|
211 |
209 |
|
2311 |
2309 |
|
233311 |
233309 |
|
28230511 |
28230509 |
|
3698196811 |
3698196809 |
|
558427718311 |
558427718309 |
|
101075417014111 |
101075417014109 |
|
19305404649695011 |
19305404649695009 |
|
6042591655354538131 |
6042591655354538129 |
|
2133034854340151959891 |
2133034854340151959889 |
|
795622000668876681038971 |
795622000668876681038969 |
|
304723226256179768837925511 |
304723226256179768837925509 |
|
221533785488242691945171845771 |
221533785488242691945171845769 |
|
167701075614599717802495087247891 |
167701075614599717802495087247889 |
Results
For all above sequences the following qestions have
been studied:
- How many terms are
prime?
- Is the Smarandache Series
convergent?
- Is the Smarandache
Infinite product convergent?
- Is the Smarandache
Simple Continued Fractions convergent?
- Is the Smarandache
Continued Radicals convergent?
For this purpose the software package Ubasic Rev. 9
has been utilized. In particular for the item n. 1, a strong pseudoprime test
code has been written [5]. Moreover, as already mentioned above, the item 5 has
been introduced for the first time; a Smarandache Continued Radicals is defined
as follows:
![]()
where a(n) is the nth term of a Smarandache
sequence. Here below a summary table of the obtained results:
|
|
# Primes |
SS_cv |
SIP_cv |
SSCF_cv |
SCR_cv |
|
Square 1st kind |
12/456=0.026 |
0.7288315379 .. |
0 |
2.1989247812 . |
2.3666079803 . |
|
Square 2nd kind |
1/463=0.0021 |
|
|
0.3301888340 . |
1.8143775546 . |
|
Cubic 1st kind |
@ |
0.6157923201 .. |
0 |
2.1110542477 . |
2.6904314681 . |
|
Cubic 2nd kind |
@ |
|
|
0.1427622842 . |
2.2446613806 . |
|
Factorial 1st kind |
5/70=0.071 |
0.9137455924 .. |
0 |
2.3250021620 . |
2.2332152218 . |
|
Factorial 2nd kind |
2/66=0.033 |
|
|
0.9166908563 . |
1.6117607295 . |
|
Palprime 1st kind |
10/363=0.027 |
0.5136249121 .. |
0 |
3.1422019345 . |
2.5932060878 . |
|
Palprime 2nd kind |
9/363=0.024 |
1.2397048573 .. |
0 |
1.1986303614 . |
2.1032632883 . |
Legend:
# primes (Number of primes/number of sequence terms
checked)
SS_cv (Smarandache Series convergence value)
SIP_cv (Smarandache Infinite Product convergence
value)
SSCF_cv (Smarandache Simple Continued Fractions
convergence value)
SCR _cv (Smarandache Continued Radicals convergence
value)
@ (This sequence contain only one prime as proved
by M. Le and K. Wu [6] )
About the items 2,3,4 and 5 according to these results
the answer is: yes, all the analyzed sequences converge except the Smarandache
Series and the Smarandache Infinite product for the square product (2nd
kind), cubic product (2nd kind) and factorial product (2nd
kind). In particular notice the nice result obtained with the convergence of
Smarandache Simple Continued Fractions of Smarandache palprime product sequence
of the first kind.
The value of convergence is roughly![]() with the first two decimal digits
correct.
with the first two decimal digits
correct.
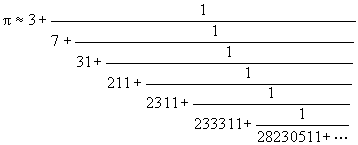
![]()
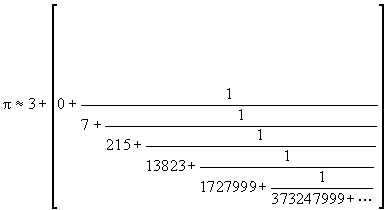
Analogously for the cubic product sequence of the
second kind the simple continued fraction converge roughly to ![]() , while for the factorial product
sequence of the second kind the continued radical converge roughly (two first decimal
digits correct) to the golden ratio
, while for the factorial product
sequence of the second kind the continued radical converge roughly (two first decimal
digits correct) to the golden ratio ![]() , that is:
, that is:
![]()
About the item 1, the following table reports the
values of n in the sequence that generate a strong pseudoprime number and its
digits number.
|
|
n |
d |
|
Square 1st kind |
1/2/3/4/5/9/10/11/1324/65/76 |
1/1/2/3/5/12/14/16/20/48/182/223 |
|
Square 2nd kind |
2 |
1 |
|
Cubic 1st kind |
1 |
1 |
|
Cubic 2nd kind |
2 |
1 |
|
Factorial 1st kind |
1/2/3/7/14 |
1/1/2/125/65 |
|
Factroial 2nd kind |
3/7 |
2/12.. |
|
Palprime 1st kind |
1/2/3/4/5/7/10/19/57/234 |
1/1/2/3/4/8/15/39/198/1208 |
|
Palprime 2nd kind |
2/3/4/5/7/10/19/57/234 |
1/2/3/4/8/15/39/198/1208 |
Please note that the primes in the sequence of
palprime of the first and second kind generate pairs of twin primes. The first
ones follow:
(3,5) (5,7) (29,31) (209,211)
(2309,2311) (28230509,28230511) (101075417014109,101075417014111)
..
Due to the fact that the percentage of primes found
is very small and that according to Prime Number Theorem, the probability that
a randomly chosen number of size n is prime decreases as 1/d (where d is the
number of digits of n) we are enough confident to pose the following
conjecture:
![]() The
number of primes contained in the Smarandache Square product sequence (1st
and 2nd kind), Smarandache Factorial product sequence (1st
and 2nd kind) and Smarandache Palprime product sequence (1st
and 2nd kind) is finite.
The
number of primes contained in the Smarandache Square product sequence (1st
and 2nd kind), Smarandache Factorial product sequence (1st
and 2nd kind) and Smarandache Palprime product sequence (1st
and 2nd kind) is finite.
New Questions
![]() Is there any
Smarandache sequence whose SS, SIP, SSCF and SCR converge to some known
mathematical constants?
Is there any
Smarandache sequence whose SS, SIP, SSCF and SCR converge to some known
mathematical constants?
![]() Are all the
estimated convergence values irrational or trascendental?
Are all the
estimated convergence values irrational or trascendental?
![]() Is there for
each prime inside the Smarandache Palprime product sequence of the second kind
the correspondent twin prime in the Smarandache Palprime product sequence of
the first kind?
Is there for
each prime inside the Smarandache Palprime product sequence of the second kind
the correspondent twin prime in the Smarandache Palprime product sequence of
the first kind?
![]() Are there any
two Smarandache sequences a(n) and b(n) whose Smarandache Infinite Product
ratio converge to some value k different from zero?
Are there any
two Smarandache sequences a(n) and b(n) whose Smarandache Infinite Product
ratio converge to some value k different from zero?
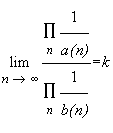
![]() Is there any
Smarandache sequence a(n) such that:
Is there any
Smarandache sequence a(n) such that:
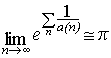
![]() For the four
sequences of first kind a(n), study:
For the four
sequences of first kind a(n), study:
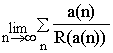
where R(a(n)) is the reverse of a(n). (For example
if a(n)=17 then R(a(n))=71 and so on).
References
[1] F. Iacobescu, Smarandache partition type and
other sequences, Bull. Pure Appl. Sci. Sec. E16(1997), No. 2, 237-240.
[2] C. Ashbacher, Smarandache Series convergence, to
appear
[3] See
http://www.gallup.unm.edu/~smarandache/product .txt
[4] C. Zhong, On Smarandache Continued fractions,
Smarandache Notions Journal, Vol. 9, No. 1-2, 1998, 40-42
[5] D.M. Bressoud, Factorization and primality testing,
Springer Verlag, 1989, p. 77
[6] M. Le and K. Wu , The primes in the Smarandache
Power product Sequence, Smarandache Notions Journal, Vol. 9, No. 1-2, 1998,
97-97